Vertical Alignment-Crest Vertical Curves
A crest vertical curve is present when a shared use path (or a roadway) goes uphill and then goes downhill. The minimum length for a crest vertical curve is a function of the stopping sight distance, the algebraic difference in the upgrade and downgrade grades, the assumed height of an object on the pavement, and the user's eye height. The AASHTO Green Book (p. 271) gives equations for calculating the minimum length of a crest vertical curve so that adequate sight distance is available, as shown below.(29)
Case 1-Sight distance greater than length of vertical curve (S>L)
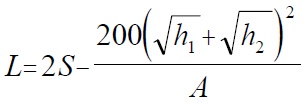
(9)
Case 2-Sight distance less than lenght of vertical curve (S>L)
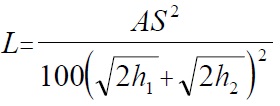
(10)
For both equations,
L = length of vertical curve (ft)
S = sight distance (ft)
A = algebraic difference in grades (percent)
h1 = height of eye (ft)
h2 = height of object (ft)
The AASHTO Guide for the Development of Bicycle Facilities (p. 36) recommends a maximum grade of 5 percent.(2) With higher grades, many bicyclists may have difficulty climbing and they may end up going downhill too fast for comfort or safe operation. A maximum grade of 5 percent also provides usable conditions for pedestrians in wheelchairs, whereas steeper grades do not. An uphill grade of 5 percent followed by a downhill grade of 5 percent results in a difference in grades of 10 percent.
Table 20 shows the calculated minimum length of crest vertical curve for each user type, using the values of "A" (the algebraic difference in grades) as described above. In addition, the sight distance was obtained by calculating the distance traveled during the perception-reaction time (using the 85th percentile observed speeds from the speed station) to the calculated braking distance under wet pavement conditions. Because the friction factor on wet pavement is one-half that on dry pavement, the 85th percentile observed braking distances were doubled to obtain the "wet" braking distances. The height of eye is the 85th percentile eye height for each user type. The height of object is zero.
Table 20. Minimum length of crest vertical curve.
| USER TYPE | 85TH PER SPEED (m/sec) | 85TH PER EYE HEIGHT (m) | STOPPING DISTANCE (m) | LENGTH OF VERTICAL CURVE (m) |
|---|---|---|---|---|
| Bicycle | 6.1 | 1.5 | 25.2 | 20.4 |
| Hand cycle | 5.2 | 0.8 | 19.2 | 21.7 |
| Inline skates | 6.4 | 1.6 | 35.6 | 38.5 |
| Kick scooter | 4.1 | 1.3 | 19.9 | 13.0 |
| Manual wheelchair | 2.3 | 1.2 | 8.5 | 0 |
| Power wheelchair | 3.1 | 1.2 | 10.2 | 0 |
| Recumbent bicycle | 8.2 | 1.2 | 33.2 | 46.7 |
| Segway | 4.6 | 1.8 | 16.1 | 0 |
| AASHTO bicycle | 8.9 | 1.5 | 38.7 | 49.8 |
The recumbent bicyclist would be the critical user for determining the minimum length of a crest vertical curve. For example, using the 85th percentile stopping distance and height of eye, the minimum length of a crest vertical curve with an algebraic difference in percent grade of 10 would be 46.7 m (153 ft).
In contrast, the AASHTO minimum length of a crest vertical curve for a bicycle with its presumed 38.6-m (127-ft) stopping sight distance is 49.8 m (163 ft). However, the FHWA study's observed stopping sight distances for bicyclists yields a required length of a crest vertical curve of only 20.4 m (67 ft) (on wet pavement).

User Comments/Questions
Add Comment/Question